What is percentage
- August 12, 2024
- Posted by: admin
- Category: Mathematical Literacy Notes

In this page you will learn about What is percentage. Study or download the notes with questions and answers.

Also Checkout 👇
Join and follow our social media accounts to stay ahead of the curricula for Mathematics, Mathematical Literacy and more subjects. with our termly updates. Get access to notes, exercises, past question papers, and more learning resources tailored specifically for Grade 10, 11, and 12 students.
About percentages
In these notes you are going to be able to practice the questions based on percentages . Make sure to practice all the questions so that you get used to solving problems of this nature.
![]()
Note that “What is percentage” is a sub topic and you can also access more notes, questions and answers under the main topic “Operations On Numbers And Calculator Skills” which is one of the recommended learning topics in the Mathematical Literacy Curriculum.
What is percentage
What is percentage?
A percentage is a way of expressing a number as a part of a whole, specifically out of 100. It is symbolized by “%”. For example, if you scored 80 out of 100 on a test, your score would be 80%, meaning you got 80% of the questions correct. Percentages are commonly used in everyday situations, such as calculating discounts, understanding statistics, and comparing quantities.
Example:
1. ![]()
![]()
2.![]()
![]()
Note that you are expected to round percentages to two decimal places unless the question specifically states otherwise.
Why? It ensures consistency, making it easier to compare values and reduces the risk of misinterpretation or errors, especially in financial or statistical contexts.
Increase a value by a certain percentage
Here are two ways to increase an amount by a specific percentage:
Example: Increase R450 by 12%
METHOD 1: Determine the increase and add it to the initial amount.
Calculating Increase
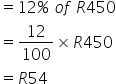
Calculating total amount
= original amount + increase
= R450 + R54
= R504
METHOD 2: Multiply the original amount by (100% + % increase)
Total = Original amount x (100% + % Increase)
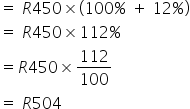
![]()
Note in this case you should treat 100% as the original amount.
Before you continue check it out 👇
Download our free PDF text books for Maths, Maths Lit and other subjects for various grades!
Continue from here👇
Decrease a value by a certain percentage
You can also use two different methods to reduce an amount by a specific percentage:
Example: Decrease R450 by 12%
METHOD 1: Determine the decrease and then subtract it from the original amount.
Calculating The Decrease
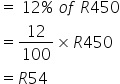
Calculating Total Amount
= original amount – decrease
= R450-R54
= R396
METHOD 2: Multiplying the original amount by (100% – % decrease)
Total = original amount x (100% – % decrease) = R450 x (100% -12%)
= R450 x (100% -12%)
= R450 x 88%

Example exercises
1. Julia earned 94 points out of 150 on her preliminary exam. What percentage does that represent?
![]()
2. In 2014, a truck is priced at R220,000. If the price increases by 8.5% per year, what will the cost of the truck be in 2015?
METHOD 1: Increase

METHOD 2: New total cost
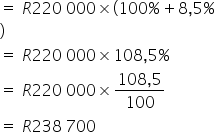
3. A boat valued at R460,000 depreciates by 4.8% per year. Calculate its value after one year.
METHOD 1:
Calculating decrease
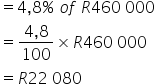
Total amount
= R460 000 – R22 080
= R437 920
METHOD 2:
Total amount
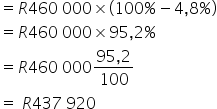
![]()
Note that you are expected to round percentages to two decimal places unless the question specifically states otherwise.
Why? It ensures consistency, making it easier to compare values and reduces the risk of misinterpretation or errors, especially in financial or statistical contexts.
Before you continue also check this out 👇
Get 100% on your exam essays using our essay cramming assistant!
It is useful if you want to cram essays for subjects such as
Business Studies, Economics, Geography, History, Home Languages, First Additional Languages and more…
Why use it?
Helps you structure how you write essays√
Helps you memorize and recall points and sentences including hints√
Marks your essays as you practice writing√
Continue from here👇
How to calculate a percentage increase?
You can determine the percentage increase of a quantity using this general formula:
![]()
Example: Calculate the percentage increase in the cost of a lollipop from R2.50 in 2014 to R3.50 in 2015.
![]()
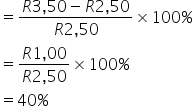
How to calculate a percentage decrease?
Determine the percentage decrease in a quantity using this general formula:
![]()
Example:
In 2005, the rhino population was 12,800, but it dropped to 8,700 in 2006. Calculate the percentage decrease in the rhino population.

Example exercises
1.What is the percentage markup on a pair of socks if it costs R38 and is sold for R120?
![]()
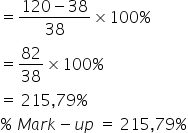
2. A plot of land was purchased for R275,000, but the owner could only sell it for R220,000. Calculate the percentage loss the owner incurred from this sale.
![]()
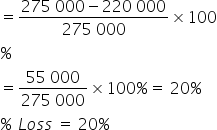
How to calculate discounts?
1. Calculating the discount
Calculate the percentage value of the discount based on the original price
Example:
A pair of soccer boots, originally priced at R1,500, is being offered with a 15% discount. Calculate the amount of the discount.
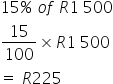
2. Calculating the sale price
Reduce the original price by the amount of the percentage discount.
Example:
A pair of soccer boots, originally priced at R1,500, is being offered with a 15% discount. Calculate the sale price.
METHOD 1
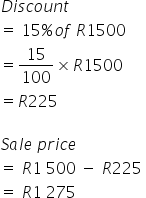
METHOD 2
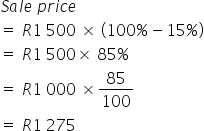
![]()
Note that 100% represents the original price, so 85% reflects the sale price after the discount has been applied.
How to calculate the original price
Example:
A pair of soccer boots is priced at R1,275 after a 15% discount. What was the original price before the sale?
Below are the two methods you can use to determine the original price:
METHOD 1: Ratio method
sale price : original price
…….% : 100%
R… : R ?
sale price : original price
85% : 100%
R1 275 : R ?
85 : 100
Hint: divide both sides by 85
1 : …
Hint: multiply both sides by 1275
1275 : ?
Original Price = (100 – 85) x 1 275
= R1 500
METHOD 2: Equation method
original price x (original % – discount %) = sale price
original price = sale price + (original % ÷ discount %)
= R1 275÷(100%-15%)
= R1 275 ÷ 85%
![]()
= R1 500
Example exercise
1. Green House Nursery sells a tray of seedlings for R12.99. If the nursery offers a 10% discount, calculate the following:
1.1 Discount
1.2 Sale Price
Answers:
1.1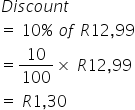
![]()
Note that R12,99 should be rounded to two decimal places when dealing with rand and cents.
1.2
Method 1
Sale Price
= original price – discount
= R12,99-R1,30
= R11,69
Method 2
Sale Price
= original price x (original % – discount %)
= R12,99 x (100%-10%)
= R12,99 x 90% = R11,69
2. If a bush of herbs was on sale for R52.99 with a 10% discount, what was the original price before the discount?
Answers:
Method 1
sale price : original price
90% : 100%
Hint: divide both sides by 90
![]()
Note
Original price = 100%
Sale price = 90%
(100% -10%):
1 : ….
Hint: multiply by 52,99
52,99 : ?
Original price = (100 ÷ 90) x 52,99 = R58,88
Method 2
original price x (original % – discount %) = sale price
Original price = sale price ÷ (original % – discount %)
= R52,99 ÷ (100% -10%)
= R52,99 ÷90%
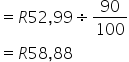
Mixed Exercises
1. Who pays higher bank fees for a deposit of R760 based on the following fee structures:
- Lungi, who pays R2.50 plus 0.75% of the deposited amount.
- Lethu, who pays R1.50 plus 0.85% of the deposited amount.
2. Calculate the increase on 1 255 kg by 16%.
3. An art store is going out of business and has decided to mark down their art pieces by 75%. Calculate the sale price of an art piece originally priced at R350.
4. In 2011, 5,600,000 South Africans were living with HIV/AIDS, and by 2012, this number had increased to 6,100,000. Determine the percentage increase in the number of South Africans living with HIV/AIDS.
5. South African exports generated a total income of R314.927 million in 2002 and R273.127 million in 2003. Calculate the percentage decrease in the total income generated by South African exports.
6. A batch of marble floor tiles was sold for R1,800 after a 20% discount was applied. What was the original price of the tiles before the discount?
7. If a desktop valued at R6,999 depreciates by 4% per year, what will its value be after 1 year?
8. Determine Sino’s percentage profit if it cost her R1,150 to create a matric dance dress, and she sold it for R2,400.
9. A window installer charges R35.90 per hour for labour. However, on Saturdays, he charges 50% more than his usual rate. He worked six hours on both Friday and Saturday. His invoice states that he is owed R638.50 for his work. Determine if the invoiced amount is accurate.
10. The Agricultural Research Council reports that 80% of South Africa’s land is used for farming. However, only 11% of this farmland is suitable for growing crops.

how much of this area is actually suitable for crop cultivation?
Answer:
1.
\[Lungi\\=R2,50\;+\;0,75\%\;of\;R760\\=R2,50+\frac{0,75}{100}\times R760\\=R2,50\;+\;R5,70\\=R8,20\]
\[Lethu\\=\;R1,50\;+\;0,85\%\;of\;R760\\=R1,50\;+\frac{0,85}{100}\times R760\\=R1,50+R6,46\]
Lungi pays higher bank fees.
2.
\[=\frac{10}{100}\times1\;255\;kg\\=200,8\;kg\\Total\;=\;1\;255\;+\;200,8\;kg\;\\=\;1\;455,8\;kg\]
OR
\[Total\;=\;1\;255\;kg\;\times\;(100\%\;+\;16\%)\;\\=\;1\;255\;\times\;116\%\\=\;1\;255\;\times\frac{116}{100}\\=1455,8\;kg\]
3.
\[Discount\;=\;75\%\;of\;R350\\=\frac{75}{100}\times R350\\=\;R262,50\\\\Sale\;price\;\\=\;R350\;-\;R262,50\;\\=\;R87,50\]
OR
\[Sale\;Price\;\\=\;R350\;\times\;(100\%\;-\;75\%)\\=\;R350\times25\%\\=\;R350\times\frac{25}{100}\\=\;R87,50\]
4.
\[\%\;Increase\\=\frac{6\;100\;000-5\;600\;000}{5\;600\;000}\times100\%\\=\frac{500\;000}{5\;600\;000}\times100\%\\=\;8,9\%\\\]
5.
\[\%\;Decrease\;\\=\frac{314\;927\;million\;-\;273\;127\;million}{314\;927\;million}\times100\%\\=\frac{41\;800\;million}{314\;927\;million}\times100\%\\=\;13,27\%\\\]
6.
Sale Price : Original Price
80% : 100%
Divide by 80
1 :...
multiply by 1800
Original Price = (100÷80) x 1 800
= R2 250
OR
Original Price = R1 800 ÷ (100% - 20%)
= R1 800 ÷ 80%
= R2 250
7.
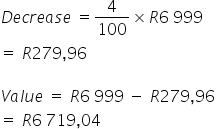
OR

8.

9.
\[Saturday's\;charge:\\Increase\;=\frac{50}{100}\times R35,90\\=\;R17,95\\\\Total\;=\;R35,90\;+\;R17,95\;\\=\;R53.85\\\]
OR
\[Total\;\\=\;R35,90\times(100\%\;+\;50\%)\\=\;R35,90\times\;150\%\\=\;R35,90\times\frac{150}{100}\\=\;R53,85\\\]
Friday's labour = R35,90x6 h = R215.40
Saturday's labour = R53,85x6h = R323,10
Total labour cost = R215,40 + R323.10
= R538,50
His invoice of R638.50 was incorrect.
10.
\[Area\;used\;for\;farming\;\\=\frac{80}{100}\times1\;219\;090\;km^2\\=\;975\;272\;km^2\]
Area used for farming
\[Area\;used\;for\;farming\;\\=\frac{11}{100}\times975\;272\;km^2\\=107\;279,92\]
Practice More Questions Like TheseBefore you continue check it out 👇
Want To Master Percentage Calculations?
Sign up for free and complete more quizzes to help you
master this topic.

Continue from here👇
Other Maths LIT Notes
Do you have any query regarding Questions and/or Answers? Let us know👇
Other Practicing Material
- Newest
- Oldest
- Most Viewed














