Types Of Numbers
In this page you will learn about Types Of Numbers, a Mathematics Paper 1 topic that is also a recommended learning topic for grade 10 students. Study or download the notes with questions and answers.
or
Also Checkout 👇
Join and follow our social media accounts to stay ahead of the curricula for Mathematics, Mathematical Literacy and more subjects. with our termly updates. Get access to notes, exercises, past question papers, and more learning resources tailored specifically for Grade 10, 11, and 12 students.
About Types Of Numbers
In these notes you are going to be able to learn about Types Of Numbers and go through exercises to practice calculating and solving relevant questions. Make sure to go through all the notes, questions and answers so that you get used to solving questions of this topic.
Note that “Types Of Numbers” is a sub topic and you can also access more grade 10 notes, questions and answers under the main topic “Numbers And Number Patterns” which is one of the recommended learning topics in the Grade 10 Mathematics Curriculum. Â Â
Introduction
In this topic it is important to keep in mind that numbers come in various forms: some are integers, others are fractions; some are positive, while others are negative.
What does Irrational mean?
\[Since\;\sqrt1\;=\;1\;and\;\sqrt4\;=\;2\\Therefore\;\sqrt3\;has\;a\;value\;between\;1\;and\;2\;thus,\sqrt3=1…\;\\and\;3\;being\;closer\;to\;4\;than\;1\;i.e\;\sqrt3=1,7\]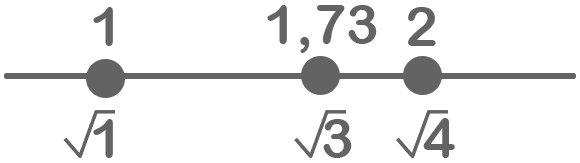
This number is indeed real! However, we can only determine its approximate value. You’ll see that the digits after the decimal point don’t follow any pattern and continue indefinitely.
\[And\;also\;for\;ins\tan ce\;\frac2{11}=18181818\\It\;also\;goes\;on\;and\;on,\;but,\;\\there\;is\;a\;pattern\;so\;it\;is\;an\;infinite,\;RECURRING\;decimal\\\\compared\;to\;\sqrt3\;=\;1,732050808\;is\;an\;infinite,\;NON-RECURRING\;decimal.\]Irrational numbers are decimals that go on forever without repeating or forming any predictable pattern.
Other examples of irrational numbers
\[\sqrt{15}\;;\;\sqrt[3]{10}\;;\;\mathrm\pi(3,141592654)\\\mathrm\pi=\frac{\mathrm{the}\;\mathrm{circumference}\;\mathrm{of}\;\odot\;}{\mathrm{the}\;\mathrm{diameter}\;\mathrm{of}\;\mathrm{the}\odot}\]Â
Also note thatÂ
\[\frac{22}7=3,142857\;142857\;is\;\;Infinite\;and\;Recurring\\and\;\frac{22}7\;and\;3,14\;are\;both\;RATIONAL\;numbers\;\\which\;are\;very\;useful\;as\;approximate\;values\;for\;\mathrm\pi.\\However,\;\mathrm\pi\;is\;IRRATIONAL!\]Before you continue check it out 👇
Want To Master Types Of Numbers Calculations?
Sign up for free and complete more quizzes to help you
master this topic.
Continue from here👇
Converting a repeating decimal into a fraction: A step-by-step guide
Example:
\[\;0,\overset.3\;i.e.\;0,333….\\Let\;x\;=\;0,333….(1)\\10x\;=\;3,3333….(2)\\9x\;=\;3\\x=\frac39=\frac13\\\;0,\overset.{3\;}=\frac13\]Now try:
\[Now\;try:\;\\(1)\;0,\overset.4\\(2)\;0,\overset.7\\(3)\;0,\overset.3\overset.1\\(4)\;0,\overset.1\overset.8\\(5)\;0,\overset.9\overset.3\]Answers:
(1)Â
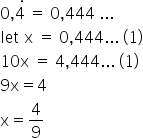
Conjecture:
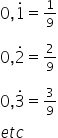
(2)
(3)
(4)
(5)
The key to turning infinite decimals into fractions lies in their recurring nature—specifically, the existence of a repeating pattern.
Before you continue also check this out 👇
Get 100% on your exam essays using our essay cramming assistant!
It is useful if you want to cram essays for subjects such as
Business Studies, Economics, Geography, History, Home Languages, First Additional Languages and more…
Why use it?
Helps you structure how you write essays√
Helps you memorize and recall points and sentences including hints√
Marks your essays as you practice writing√
Continue from here👇
Scientific Notation
What is a Rational Number?
A rational number is a number that can be expressed as a ratio or quotient of two integers.
Example exercises
(Attempt to work through these examples on your own first.)
- 5
- -2
- 4,1
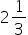
- 3,14
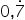
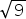
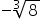
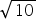
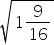
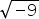
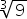
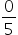
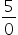
Answers
TYPES OF NUMBERS & THE NUMBER LINE
Imagine a line stretching infinitely in both directions, and now picture placing every whole number along this line.
Next, input all remaining rational numbers, such as fractions—both common and decimal forms. The spaces are reserved for irrational numbers.
Let’s now introduce the irrational numbers:
With these, our number line becomes complete, representing the entire set of REAL numbers.
Is every number a real number?
So therefore there’s no number equal -16 when squared
And also Real numbers + Non-real numbers = Complex numbers
Before you continue check it out 👇
Download our free Grade 10 Mathematics PDF text book!
Continue from here👇
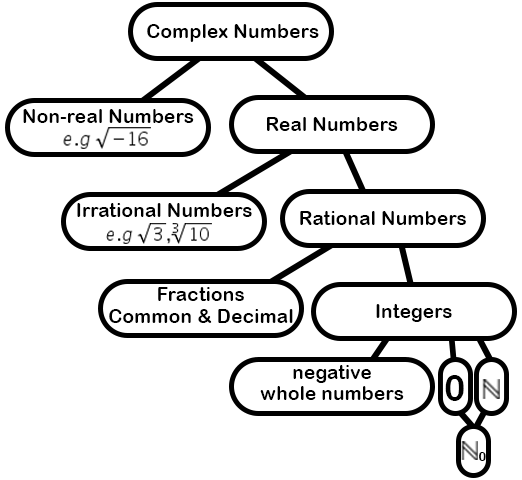
The Number Tree
Â
No need to concern yourself with complex numbers right now—what’s crucial is grasping the organization of the NUMBER SYSTEM.!
Lets also classify previous example exercise numbers
| Â | Complex | Non-real | Real | Irrational | Rational | Integer | No | N |
| 1 | ✓ |  | ✓ |  | ✓ | ✓ | ✓ | ✓ |
| 2 | ✓ |  | ✓ |  | ✓ | ✓ |  |  |
| 3 | ✓ |  | ✓ |  | ✓ |  |  |  |
| 4 | ✓ |  | ✓ |  | ✓ |  |  |  |
| 5 | ✓ |  | ✓ |  | ✓ |  |  |  |
| 6 | ✓ |  | ✓ |  | ✓ |  |  |  |
| 7 | ✓ |  | ✓ |  | ✓ | ✓ |  |  |
| 8 | ✓ |  | ✓ |  | ✓ | ✓ |  |  |
| 9 | ✓ |  | ✓ | ✓ |  |  |  |  |
| 10 | ✓ |  | ✓ |  | ✓ |  |  |  |
| 11 | ✓ | ✓ |  |  |  |  |  |  |
| 12 | ✓ |  | ✓ | ✓ |  |  |  |  |
| 13 | ✓ |  | ✓ |  | ✓ | ✓ | ✓ |  |
| 14 | Â | Division | by | zero | is | undefined | Â | Â |
Mixed Exercises
1.1 Convert the following to decimals:
1.1.1 
1.1.2
1.1.3
1.2 Convert the following to common fractions
1.2.1Â 1,3
1.2.2 
1.2.3 
1.3 Rewrite the numbers in their expanded form.
i.e 
1.3.1 
1.3.2 
1.3.3 
1.3.4 
1.4 Write these numbers in dot form:
1.4.1 0,111…
1.4.2 0,454545…
1.4.3 2,789789…
1.4.4 0,7212121…
2. Indicate whether each statement is accurate or not. If it is incorrect, provide the correct version.
2.1 Every irrational number belongs to the set of real numbers.
2.2 Every fraction is a rational number.
2.3 Not all integers are natural numbers.
2.4 When any number is divided by zero, the result is undefined.
Answers Without Explanations:
1.1.1 1,2
1.1.2 4,375
1.1.3 0,636363...
1.2.1
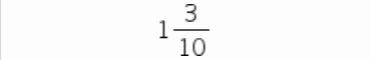
1.2.2
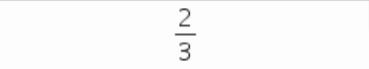
1.2.3
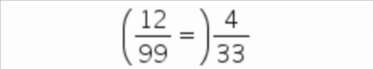
1.3.1 2,666...
1.3.2 0,515151...
1.3.30,501 501 501...
1.3.41,2333...
1.4.1
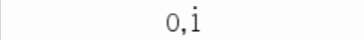
1.4.2
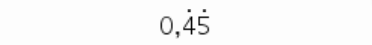
1.4.3
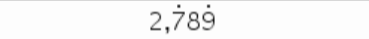
1.4.4
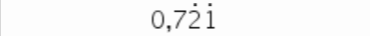
2.1 True
2.2 True
2.3 False; All natural numbers are integers.
2.4False; Division by zero is undefined
3.1
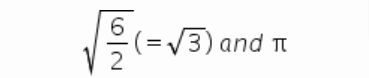
3.2
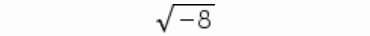
3.3
3.4
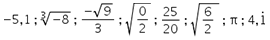
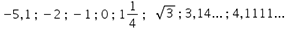
4.1
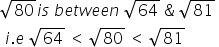
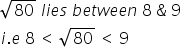
4.2
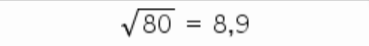See Explanations For Answers
Other Grade 10 Math Notes
Do you have any query regarding Questions and/or Answers? Let us know👇
Other Practicing Material
ENGLISH HOME LANGUAGE PAPER 1 GRADE 11 (Questions With Explained Answers) NOVEMBER 2020
