NUMBER PATTERNS Part 2 (Second Guide)
- September 9, 2024
- Posted by: admin
- Category: Mathematics Notes

In this page you will learn about NUMBER PATTERNS Part 2 (Second Guide), a Mathematics Paper 1 topic that is also a recommended learning topic for grade 10 students. Study or download the notes with questions and answers.

Also Checkout 👇
Join and follow our social media accounts to stay ahead of the curricula for Mathematics, Mathematical Literacy and more subjects. with our termly updates. Get access to notes, exercises, past question papers, and more learning resources tailored specifically for Grade 10, 11, and 12 students.
About NUMBER PATTERNS Part 2 (Second Guide)
In these notes you are going to be able to learn about NUMBER PATTERNS Part 2 (Second Guide ) as you go through notes and exercises to help you practice calculating and solving relevant questions. Make sure to go through all the notes, questions and answers and also complete the Mastery Quizzes so that you can deepen your understanding and master this topic.
![]() Note that “NUMBER PATTERNS Part 2 (Second Guide )” is a sub topic and you can also access more grade 10 notes, questions and answers under the main topic “Numbers And Number Patterns” which is one of the recommended learning topics in the South African Grade 10 Mathematics Curriculum.
Note that “NUMBER PATTERNS Part 2 (Second Guide )” is a sub topic and you can also access more grade 10 notes, questions and answers under the main topic “Numbers And Number Patterns” which is one of the recommended learning topics in the South African Grade 10 Mathematics Curriculum.
NUMBER PATTERNS Part 2 (Second Guide )
Here are two scenarios to consider.
(13) 2; 5; 8 ; 11 ; . . . CASE 1
(14) 2 ; 6 ; 18 ; 54 ; . . . CASE 2
Key questions to consider for each case:
- How does the process work?
- What are the next steps?
- What is the 10th number?
- What is the 100th number?
- What is the nth number?
Answers to (1) and (2)
In both scenarios, we begin with the number 2.
In CASE 1: we add 3 to find the following term.
In CASE 2: we multiply by 3 to determine the next term, and these processes repeat…
(2) next term:
CASE 1: 11 + 3 = 14
CASE 2: 54 x 3 = 162
![]() However, the next three questions—(3), (4), and (5)—are more challenging to address…
However, the next three questions—(3), (4), and (5)—are more challenging to address…
Let’s examine in greater detail how these figures evolved.
CASE 1 :
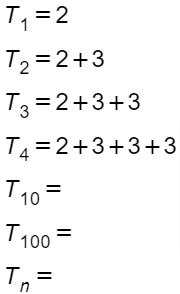
CASE 2:
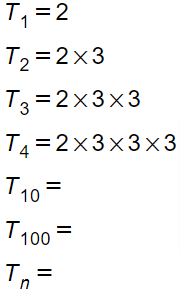
![]() So, they aren’t really that different! All the terms follow the same structure, right? And their value is determined by their position like a locker number.
So, they aren’t really that different! All the terms follow the same structure, right? And their value is determined by their position like a locker number.
n : 1 2 3 4 5 ……..20 ……..100
![]() : 2 2 + 1(3) ; 2 + 2(3) ; 2 + 3(3) ; 2 + 4(3) …;… 2 + 19(3) ….;…. 2 + 99(3)
: 2 2 + 1(3) ; 2 + 2(3) ; 2 + 3(3) ; 2 + 4(3) …;… 2 + 19(3) ….;…. 2 + 99(3)
![]()
CASE 2
n : 1 2 3 4 5 ……..20 ……..100
![]()
![]()
Answers to (3), (4), (5)
CASE 1:
(3)![]() = 2 + 9(3) = 29 ;
= 2 + 9(3) = 29 ;
(4)![]() = 2 + 99(3) = 299 ;
= 2 + 99(3) = 299 ;
(5) Tn = 2 + (n – 1)(3)
= 2 + 3n – 3
= 3n – 1
CASE 2:
![]()
![]()
![]()
![]()
![]()
![]()
OR try a different approach … but you can only see it if you log in and go through the NUMBER PATTERNS Mastery Quizzes
 Study And Practice with AI!
Study And Practice with AI!
Plug Bot is an AI you can ask questions as you go through these notes, it is programmed with math curriculum content and it can further your understanding about NUMBER PATTERNS.
Geometric Figures
![]()
Geometric figures are a rich source of number patterns because they often exhibit consistent shapes and relationships that can be translated into mathematical sequences or formulas. For example, shapes like triangles, squares, and hexagons have predictable numbers of sides, angles, or vertices, and when arranged or expanded in a series, these features create discernible patterns.
These patterns help in understanding mathematical properties such as area, perimeter, and symmetry, and they often reveal connections between geometry and algebra through sequences like the Fibonacci series or triangular numbers.
Geometric Figures
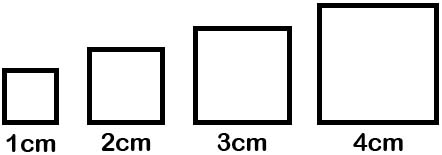
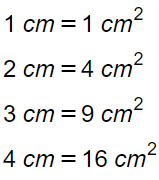
Quick exercise What are the areas of the following:
- 5th square?
- 10th square?
- 21st square?
- nth square?
Answers

Here’s how we can connect what we’ve learned using the dots:

How many dots are in the 5th, 10th, 21st, and nth figures?
you can calculate it as follows
1 = ……….
1 + 3 = ……….
1 + 3 + 5 = ……….
1 + 3 + 5 + 7 = ……….
- What is the total of the first 5 odd numbers?
- What is the total of the first 10 odd numbers?
- What is the total of the first 21 odd numbers?
- What is the total of the first n odd numbers?
Answers
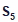 =25
=25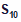 =100
=100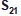 =441
=441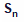 =
=
![]()
![]() : The symbol representing ‘the sum of the first n terms of a sequence’ is highly convenient, as it helps reduce the need for lengthy explanations.
: The symbol representing ‘the sum of the first n terms of a sequence’ is highly convenient, as it helps reduce the need for lengthy explanations.
RECTANGLES
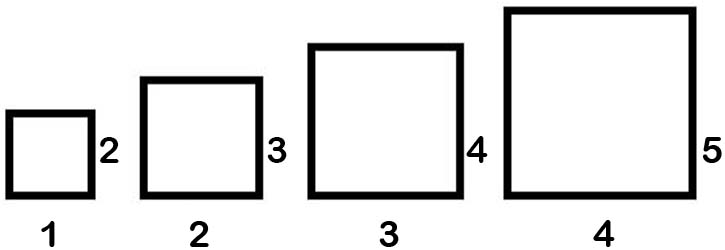
![]()
What would be the areas of:
- the 5th rectangle
- the 10th rectangle, the 21st rectangle
- and the nth rectangle?
Answers
Using Dots:

Number of dots:
….. …… ………. …………….
How many dots are in the: 5th, the 10th, the 21st, the nth figure?
Lets add even numbers as follows:
2 =…………….
2 + 4 =…………….
2 + 4 + 6 =…………….
2 + 4 + 6 + 8 =…………….
What is the total of the first 5 even numbers?…………….
What is the total of the first 10 even numbers?…………….
What is the total of the first 21 even numbers?…………….
What is the total of the first n even numbers?…………….
Answers
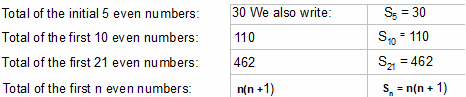
 Want To Master NUMBER PATTERNS?
Want To Master NUMBER PATTERNS?
Sign up for free and complete the Mastery Quizzes with explained answers to deepen your understanding of this topic.
TRIANGLES
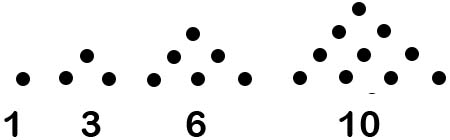
Lets add consecutive natural numbers from 1:
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
![]() We can determine the number of dots in the 5th figure by adding the sequence: 1 + 2 + 3 + 4 + 5, which equals 15.
We can determine the number of dots in the 5th figure by adding the sequence: 1 + 2 + 3 + 4 + 5, which equals 15.
But what happens after that? The 10th time? The 100th? The nth?
Let’s reintroduce the rectangles…
Below is a ‘dot patterns’ it will help us to understand our pattern:
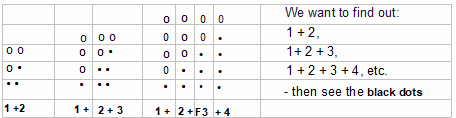
What portion of the dots is black (the ones we are focusing on)?
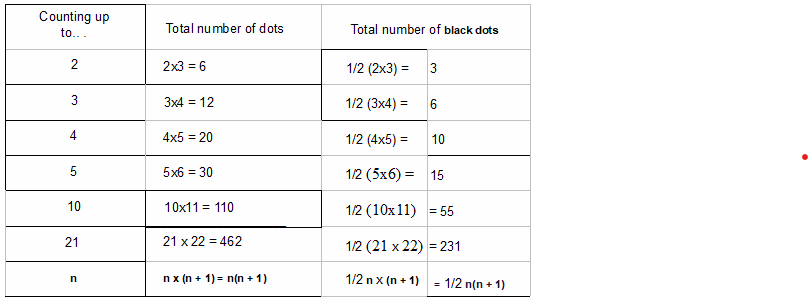
1 + 2 + 3 + 4 + . . . + n =![]()
![]()
How do we find the total of the first 100 natural numbers? In other words, what is ![]() ?
?
Answers
The number of black dots is equal to ![]() the sum/total number of dots
the sum/total number of dots
The sum of the first 100 natural numbers ![]()
POLYGONS
Now lets focus on triangle ; quadrilateral ; pentagon ; hexagon ;…
Example exercise
Here are some polygons to consider:
![]() Note that these polygons are not necessarily REGULAR, meaning their sides may not all be of equal length.
Note that these polygons are not necessarily REGULAR, meaning their sides may not all be of equal length.
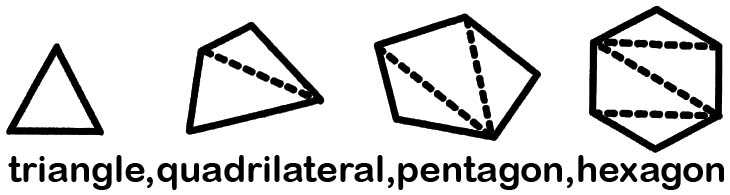
Fill in the table below by identifying the relationship between the following…
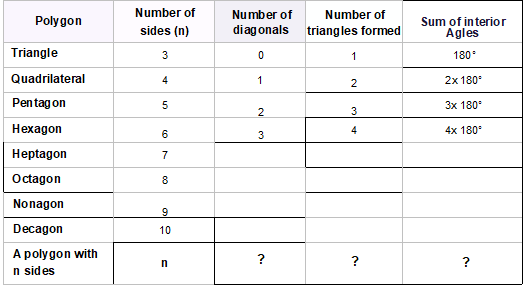
Thus, a decagon, which has ten sides, features …(a)… diagonals, …(b)… triangles, and the total of its interior angles equals …(c)… . In addition, each angle in a regular decagon measures …(d)….

 Need a Math tutor?
Need a Math tutor?
Start by joining our free sessions with professional math tutors, conducted entirely online for your convenience. Whether you’re at home or on the go, you won’t miss a thing our lessons are live and also recorded for easy access anytime. Plus, students can enquire with our tutors 24/7 for additional support.
Mixed Exercises
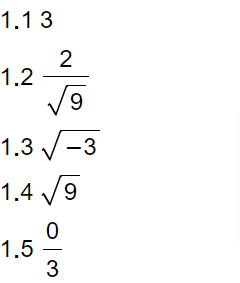
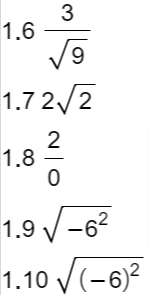
![]() Feel free to use the numbers multiple times.
Feel free to use the numbers multiple times.
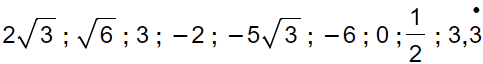

3. What are the two integers that ![]() falls between?
falls between?
4. Fill in on the gap _____ with = , > or < sign. Show working. (Do not use a calculator.)
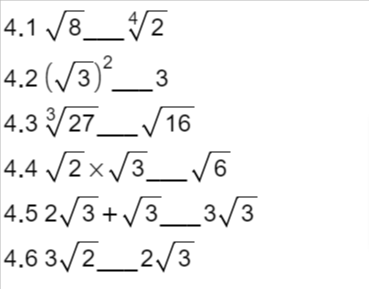
5. Draw/illustrate the given values of x on a number line.
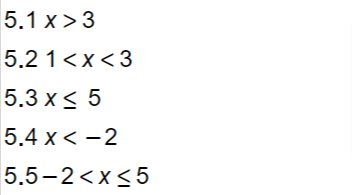
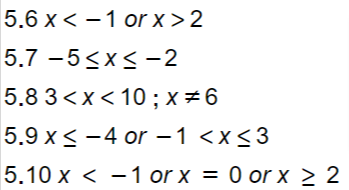
6. Express the following algebraically.
6.1 
6.2 
6.3 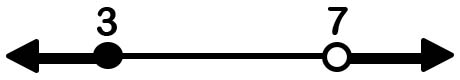
6.4 
6.5 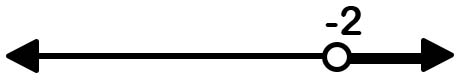
6.6 
6.7 
6.8 
6.9 
6.10 
 Ask Plug Bot!
Ask Plug Bot!
Questions you could ask Plug Bot our AI:
- How can I model a sequence with exceptions or irregularities?
- What impact does changing the initial condition have on the whole pattern?
- Are there any practical applications of sequences?
- Is there a way to check if a given number fits into the pattern?
- Can I detect a secondary pattern or structure (e.g., alternating sequences)?
- Can I create an expression to represent the pattern for any term?
Plug Bot is good at answering some of your mathematics questions andis very useful as you go through these notes, it is programmed with the South African math curriculum content and it can explain concepts and answer your questions that are relevant to this topic.
7. Match the following
e.g 7. = G

8. Simplify and express your answers in simplified surd form when needed.

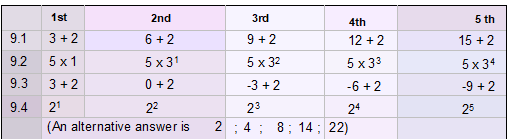
9. Determine the next two terms in the following sequences:
9.1 5 ; 8 ; 11 ; . ..
9.2 5 ; 15 ; 45 ; . . .
9.3 5 ; 2 ; -1 ; …
9.4 2 ; 4 ; 8 ; …
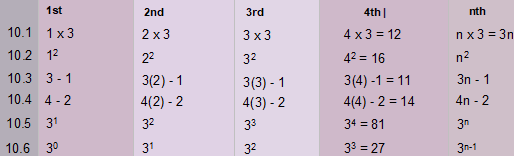
10. Determine the next term and the general formula for the ![]() term in the given sequence:
term in the given sequence:
10.1 3 ; 6 ; 9 ; …
10.2 1 ; 4 ; 9 ; …
10.3 2 ; 5 ; 8 ; …
10.4 2 ; 6 ; 10 ; …
10.5 3 ; 9 ; 27 ; …
10.6 1 ; 3 ; 9 ; …
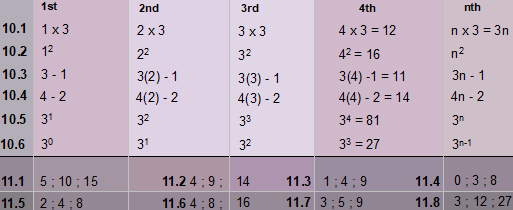
11.Provide the first three terms for each of the following sequences.
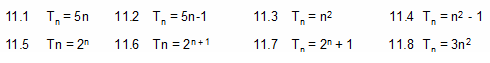
Answers:
1.
1.1 3 : real; rational; integer
1.2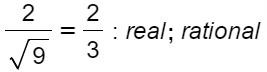
1.3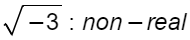
1.4
1.5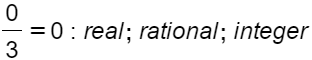
1.6
1.7
1.8
1.9
1.10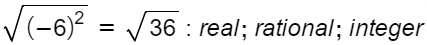
2.

3.
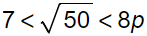
4.
4.1
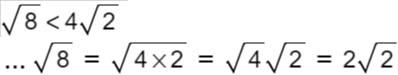
4.2
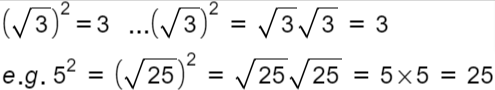
4.3
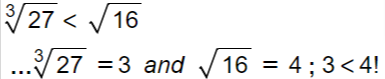
4.4
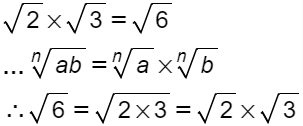
4.5
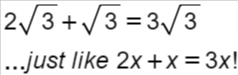
4.6
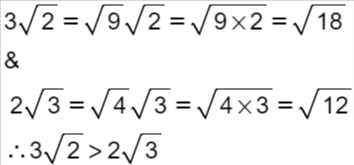
5.1

5.2

5.3

5.4

5.5

5.6


5.8
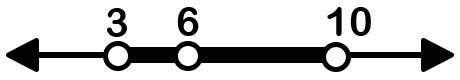
5.9

5.10

6.1 -1 < x < 4
6.2 x ≤ 5
6.3 x ≤ 3 or x > 7
6.4 3 ≤ x < 7
6.5 x > -2
6.6 -5 ≤ x ≤ -2 or x ≥ 0
6.7 -3 ≤ x < 5 ; x ≠ 2
6.8 x < -3 or 7 < x ≤ 8
6.9 x = 1 or x = 2 or x = 3 or x = 4
6.10 x = -2 or x > 5
7.
7.1 x > 3 & A. (3; ∞)
7.2 -3 ≤ x < 5 & C. [-3; 5)
7.3 x < 3 & F. (-∞; 3)
7.4 x ≥ 3 & E. [3;∞)
7.5 -3 < x ≤ 5 & D. (-3; 5]
7.6 x ≤ 3 & B. (-∞; 3]
8.
8.1 2
8.2 -5
8.3 2
8.4 -1
8.5 +5 (only)
8.6 +2 (only)
9.
9.1 14; 17
9.2 135; 405
9.3 -4; -7
9.4 16; 32
10.

10.
 Also get 100% on your exam essays!
Also get 100% on your exam essays!
Our essay cramming assistant is useful if you want to cram essays for subjects such as Business Studies, Economics, Geography, History, Home Languages, First Additional Languages and more…


