12
In this page you will learn about Analytical Geometry, a Mathematics Paper 2 topic that is also a recommended learning topic for grade 10, 11 & 12 students. Study or download the notes with questions and answers.
Also Checkout 👇
Join and follow our social media accounts to stay ahead of the curricula for Mathematics, Mathematical Literacy and more subjects. with our termly updates. Get access to notes, exercises, past question papers, and more learning resources tailored specifically for Grade 10, 11, and 12 students.
About Analytical Geometry For Grade 10, 11 & 12
In these notes you are going to be able to learn about Analytical Geometry as you go through notes and exercises to help you practice calculating and solving relevant questions. Make sure to go through all the notes, questions and answers and also complete the Mastery Quizzes so that you can deepen your understanding and master this topic.
Note that “Analytical Geometry For Grade 10, 11 & 12” is one of the mathematics topic and you can also access more grade 10,11 & 12 notes, questions and answers from the recommended learning topics in the South African Mathematics Curriculum.
Exercises
1. Given points A(-1, 3), B(7, 1), and C(x, 2) on a Cartesian plane, determine the value of x if:
1.1 
(6)
1.2 
(3)
1.3 C is the midpoint of AB. (2)
1.4 
(1)
2. Points P(4, 3), Q(4, -1), R(8, -1), and the origin, O(0, 0), are located on the Cartesian plane. Provide the following information: A sketch is necessary!
2.1
(a) the length of OP
(b) the length of PQ
(c) the length of QR
2.2
(a) the midpoint of OP
(b) the midpoint of PQ
(c) the midpoint of QR
2.3
(a) the gradient of OP
(b) the gradient of PQ
(c) the gradient of QR
2.4
(a) the equation of OP
(b) the equation of PQ
(c) the equation of QR
(12)
3.1 Given that M(2, -3) is the midpoint of line segment PQ, and the coordinates of point P are (3, 8), find the coordinates of point Q. (5)
3.2 Points A(4, 8) and B(-3, 6) are located on a Cartesian plane. Find the following:
(a) the gradient of AB. (2)
(b) the gradient of CD if CD || AB. (2)
(c) the gradient of MN if MN 
AB. (2)
3.3 Show that the points M(0, 1), N(1, -2), and P(2, -5) are collinear (lie on the same straight line). (3)
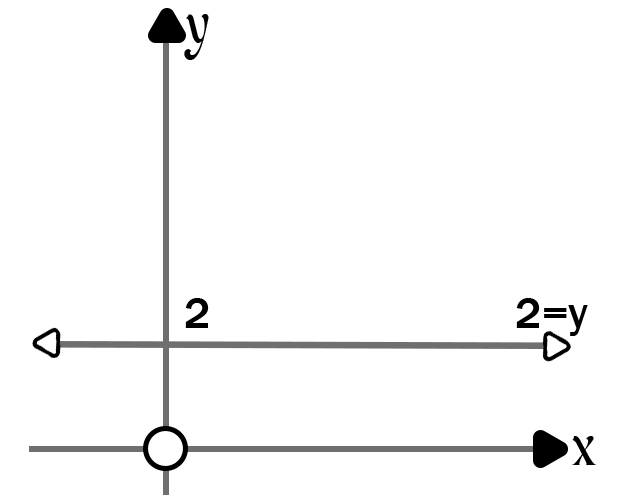
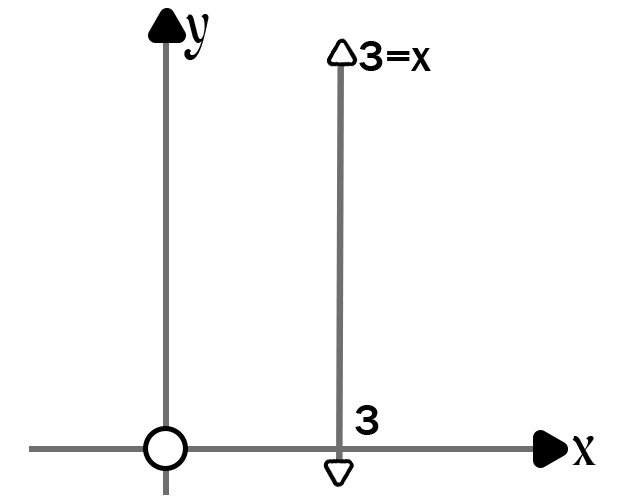
3.4 Create basic sketches of the following graphs:
(a) y = 2
(b) x = 3
(c) y = x
(d) y = -2x
(e) y = x + 1
(f) y = -x + 2
(g) x + y + 1 = 0
(h) 2x + 3y = 6
(i) 
(18)
4.1 The points A(-4, -1), R(2, 3), and M(6, -3) represent the vertices of a triangle.
(a) Find the coordinates of point S, which is the midpoint of segment AM.
(b) Derive the equation for the line passing through points R and S.
(c) Determine the distance between points R and A.
4.2 (a) Prove that triangle ARM is a right-angled triangle. (4)
(b) Demonstrate that ∠RÂM measures 45°, providing justifications for your answer.(5)
4.3 Calculate the area of ∠ARM. (2)
5. The points P(-1, 7) and Q(3, -1) are located on a Cartesian plane. Calculate:
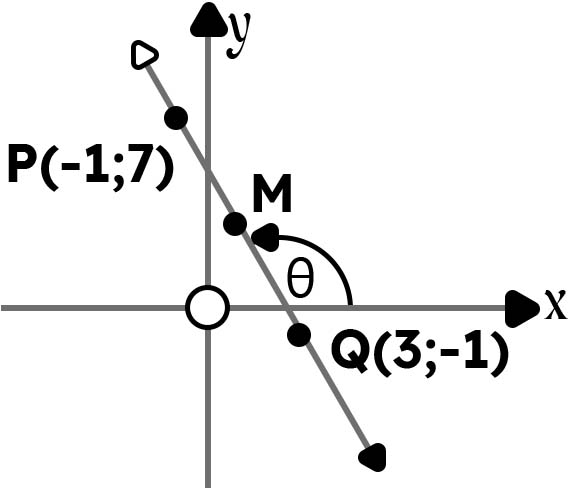
5.1 Determine the length of segment PQ and express your answer in its simplest surd form. (3)
5.2 Find the coordinates of M, the midpoint of segment PQ. (2)
5.3 Write the equation of PQ in the format y = . . . (4)
5.4 The angle formed by the line segment PQ with respect to the positive Y-axis when its size is 0. (3)
5.5 Determine the equation of the line that runs parallel to PQ and intersects at the point (-5, 1). Present the equation in the format y = … (3)
Answers:
1.1
1.2
\[\frac{2-1}{\mathcal x-7}=\frac12\\\mathcal x-7=2\\\mathcal x=9\]
1.3
\[\mathcal x=\frac{-1+7}2\\=\frac62\\=3[latex]
1.4
[latex]\mathcal x=7\]
2.1
(a) 5 units (b) 4 units (c) 4 units
2.2
(a) \[\left(2;1\frac12\right)\]
(b) (4;1)
(c) (6;-1)
2.3
(a) \[=\frac34\]
(b) undefined
(c) 0
2.4
(a) \[\mathcal Y=\frac34\mathcal x\]
(b) x = 4
(c) y = -l
3.1
By inspection : Q(1;-14)
The translation P -> M is (x - 1; y - 11) M -> Q is the same
\[\frac{3+X_Q}2=2\\3+X_Q=4\\x_Q=1\\\\\&\\\\\frac{8+Y_Q}2=-3\\8+Y_{Q=-6}\\Y_{Q=-14}\]
\[Q(1;-14)\]
3.2
(a) \[m_{AB}=\frac{6-8}{-3-4}\\=\frac{-2}{-7}\\=\frac27\]
(b) \[m_{CD}=\frac27\]
(c) \[m_{MN}=-\frac72\]
3.3
\[m_{MN}=\frac{-2-1}{1-0}\\=\frac{-3}1\\=-3\\m_{MP}=\frac{-5-1}{2-0}\\=\frac{-6}2\\=-3\]
M, N A P are collinear
(a)
(b)
(c)
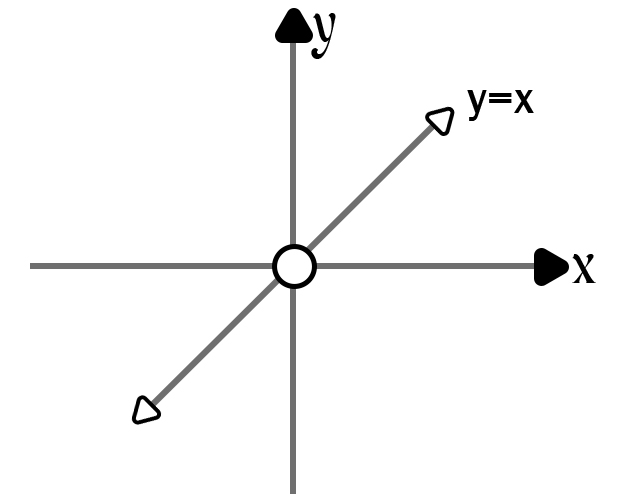
(d)
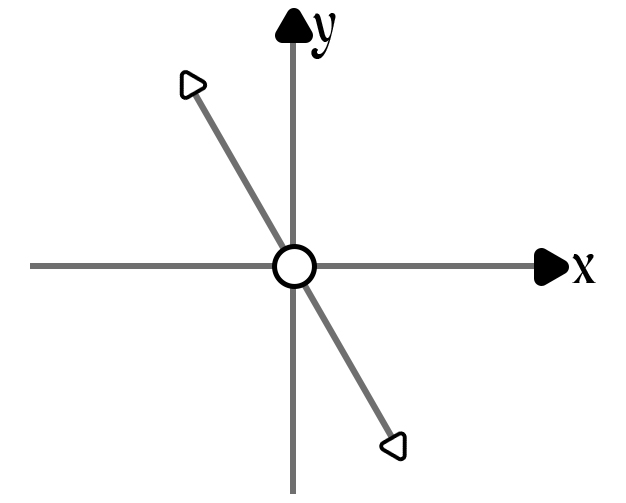
(e)
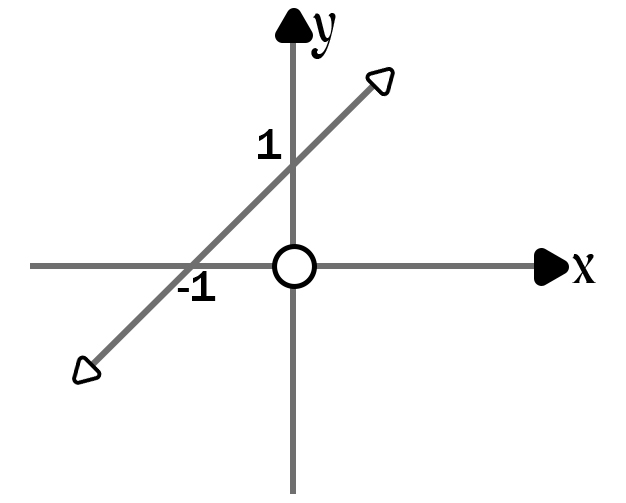
(f)
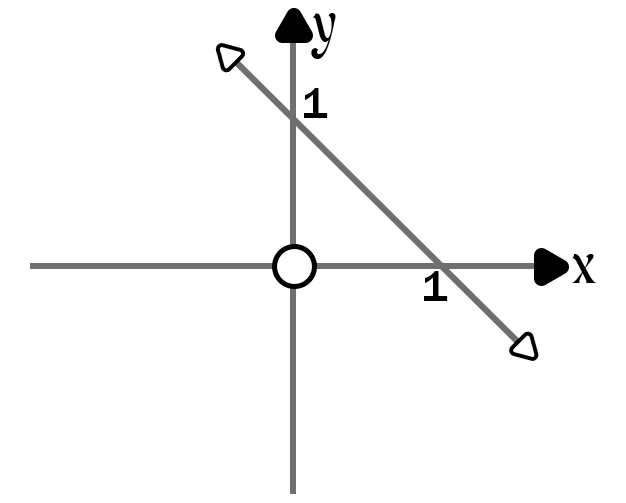
(g) x+y+l=0 y-intercept: (when x = 0) y = -1 x-intercept: (wheny = 0) x = -1 [ Use the 'dual-intercept' method ]
(h) 2x + 3y = 6 y-intercept: (when x = 0) y = 2 x-intercept: (wheny = 0) x = 3
(i) \[\frac x2-\frac y5=1\] y-intercept: (whenx = 0) y = -5 x-intercept: (wheny = 0) x = 2
4.1
(a) \[S(\frac{-4+6}2;\frac{-1-3}2)\] S(1;-2)
(b) \[M_{RS}=\frac{3-(-2)}{2-1}\\=\frac51\\=5[/latex
Equaction of RS
y = mx + c 3 = (5)(2) + c -7 = c Equation: y = 5x - 7
OR
Substitute m=5 & point (2; 3) in y - y1 = m(x - x1) y-3 = 5(x-2) y-3 = 5x -10 y = 5x - 7
(c)[latex]{RA}^2={(2+4)}^2+{(3+1)}^2\\=6^2+4^2\\=36+16\\=52\\RA=\sqrt{52}\\RA=7,21\;uunits\]
4.2
(a) \[m_{AR}=\frac{3-(-1)}{2-(-4)}\\=\frac46\\=\frac23\]
&
\[m_{RM}=\frac{3-(-3)}{2-6}\\=\frac6{-4}\\=-\frac32\\m_{AR}\times m_{RM}\\=-1\\A\widehat RM=90^\circ\\\]
∠ ARM is right-angled
(b) \[RA=\sqrt{52}\\\&\\A\widehat RM=90^\circ\\{RM}^2=\left(2-6\right)^2+\left(3+3\right)^2\\=16+36\\=52\\RM=\sqrt{52}\\\]
∠ARM is an isosceles right-angled∠ RÂM = 45°
4.3
\[Area=\frac12AR.RM\\=\frac12\sqrt{52}\sqrt{52}\\=26\;square\;units\\\]
5.1
\[{PQ}^2={(3+1)}^2+{(-1-7)}^2\\=16+64\\=80\\PQ=\sqrt{80}\\=\sqrt{16\times5}\\=\sqrt{16}\sqrt5\\=4\sqrt5\;units\\\]
5.2
\[M(\frac{-1+3}2;\frac{7+(-1)}2)\\\]
M(1;3)
Study And Practice with AI!
Plug Bot is an AI you can ask questions as you go through these notes, it is programmed with math curriculum content and it can further your understanding about ####.
6.1 Find the angle that the line 2x + 3y = 5 forms with the positive x-axis, rounded to one decimal place. (4)
6.2 Find the numerical value of p if the line represented by the equation
forms an angle of inclination of 135° with the positive direction of the x-axis. (4)
7. In the given figure, QRST is a parallelogram where the vertices Q and T are positioned on the y-axis. The side RS is extended to point U, with RS equal to SU. The distance between Q and T is 4 units, and the coordinates for points R and T are (9, 9) and (0, 3), respectively. The line segment QU crosses TS at point W.
- Find the coordinates of: (a) point Q (b) point U. (1)(2)
- Determine the equation of the line OR. (2)
- Given that W is the midpoint of line segment UQ, verify if W lies on line OR, meaning check if points O, W, and R are collinear. (4)
8. In the diagram, triangle ABC has vertices A(2, 5), B(-4, -1), and C.
T(1, 3) represents the intersection point of the altitudes (heights or perpendiculars) drawn from vertices A, B, and C.
The angle between line segment AB and the x-axis is denoted as θ. The equation of the line that passes through points C and T is y = -x + 4.
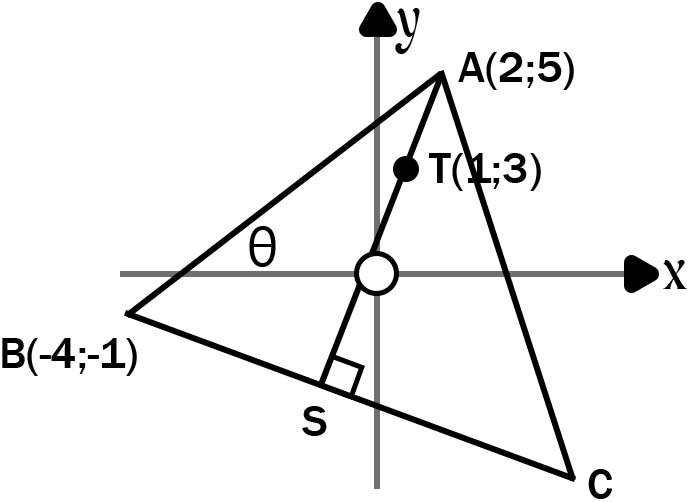
8.1 Find the length of AB, expressing your answer in its simplest surd form. (2)
8.2 Compute the value of angle θ. (2)
8.3 State the gradient of line AS. (1)
8.4 Prove that the equation for line BC is x + 2y + 6 = 0. (3)
8.5 Therefore, find the coordinates of point C. (4)
Answers:
8.1\[AB^2={(2+4)}^2+\;{(5+1)}^2=\;36+\;36\\AB\;=\;\sqrt{36\;x\;2}\;\\AB=\;\sqrt{36}\sqrt2\;\\AB=\;6\;72\;units\]
8.2\[m_{AB}=\frac{5-(-1)}{2-(-4)}\\=\frac66\\=1\]
8.3\[m_{AS}=\;2\;\;\;.....\frac{5-3}{2-1}\]
8.4\[Substitute\;m_{BC}=-\frac12\\\&\;point\;B(-4;-1)\\y=mx+c\\-1=(-\frac12)(-4)+c\\-1=2+c\\-3=c\]
Or
\[y-y_1=m(x-x_1)\\y+1=-\frac12(x+4)\\y+1=-\frac12x-2\\y=-\frac12x-3,\;etc\]
8.5Equation\;of\;BC:\\y=-\frac12x-3\\\&\;y=-x+4\\-\frac12x-3=-x+4\\\frac12x=7\\x=14\;\&\;y=-14+4=-10\\C(14;\;-10)
93x+2y+6=0\\y-intercept,\;-3\\x-intercept,\;-2\\Gradient=-.\frac32\\OR:\;S\tan dard\;form:\\2y=-3x-6\\y=-\frac32x-3
9.1=-\frac32
\[=-\frac32\]
9.2\[=+\frac23\]
10.1
\[D(-\frac12;1)\]
10.2\[m_{AB}=\frac{4-(-2)}{1-(-2)}\\=\frac63\\=2\]
\[m_{Perpendicular\;bisector}\\=-\frac12\\D(-\frac12;1)\;\\\&\\m=-\frac12\\y-y_1=m(x-x_1):\\y-1=-\frac12(x+\frac12)\\y-1=-\frac12x-\frac14\\y=-\frac12x+\frac34\\\]
10.3\[Equation\;of\;BE:\\E\;midpoint\;AC\;is\;\;E\left(2\frac12;\;2\frac12\right)\\m_{BE}=\frac{2{\displaystyle\frac12}+2}{2\frac12+2}\\\\m_{BE}=\frac{4{\displaystyle\frac12}+2}{4\frac12+2}\\m_{BE}=1\\\&\;(-2;-2)\\y+2=1(x+2)\\y=x\]
10.4\[m_{DE}=\frac{2{\displaystyle\frac12}-1}{2{\displaystyle\frac12}-(-{\displaystyle\frac12})}\\m_{DE}=\frac{1{\displaystyle\frac12}}3\\m_{DE}=\frac12\\\&\\m_{BC}=\frac{1-(-2)}{4-(-2)}\\m_{BC}=\frac36\\m_{BC}=\frac12\\DE\vert\vert BC\]
10.5 \[m_{BC}=\frac{1+2}{4+2}\\m_{BC}=\frac36\\m_{BC}=\frac12\\\beta=26,57^\circ\\\\\&\\\\m_{AB}=2\\\alpha=63,43^\circ\\A\widehat BC=\alpha-\beta\\A\widehat BC=63,43^\circ-26,57^\circ\\A\widehat BC=36,86^\circ\\\]
10.6M(-5;1)
It can be translated as C -> A is: (x; y) -> (x - 3; y + 3)
Also B -> M
M(-2-3; -2 + 3)
since "opposite sides of a parallelogram are equal and parallel "
11.1\[Midpoint\;of\;PR\;is\\T(\frac{-1+3}2;\frac{3+(-1)}2)\\T(1;1)\]
11.2m_{PR}=\frac{-1-3}{3-(-1)}\\=\frac{-4}4\\=-1\\m_{perpendicular\;bisector=1}\\Substitute\;m=1\;\\\&\;point\;(1;1)\;\\in\;y-y_1=m(x-x_1)\\y-1=1(x-1)\\y=x\\At\;S,\;a=b\;....S\;on\;line\;y=x
11.3\[Area\;of\;\triangle PRS=\frac12PR,ST=12\\Now,\;PR=\sqrt{{(3+1)}^2+{(-1-3)}^2}\\=\sqrt{2{(a-1)}^2}\\\frac12.4\sqrt2.\sqrt2\sqrt{{(a-1)}^2}=12\\4\sqrt{{(a-1)}^2}=12\\\sqrt{{(a-1)}^2}=3\\{(a-1)}^2=9\\a-1=\pm3\\a=1\pm3\\a=-2\\\\S(-2;-2)\]
11.4\[Alternative\;to\;\boldsymbol a\;in\;11.3\;is\;\\a=1+3=4\;(\&\;b\;=\;a\;=\;4)\;\therefore\\\;For\;Q(4;\;4),\;also\;on\;the\perp^r\;\\bisector\;of\;PR\;(like\;S),\;APRQ\;\\also\;has\;an\;area\;of\;\\12\;square\;units.[/latext]
TQ =TS
[latex]\boldsymbol O\boldsymbol r\boldsymbol:\\ST=\sqrt{{(-2-1)}^2+{(-2-1)}^2}\\ST=\sqrt{18}\\\&\\TQ=\sqrt{{(4-1)}^2+{(4-1)}^2}\\TQ=\sqrt{18}\\ST=TQ\\\boldsymbol O\boldsymbol r\boldsymbol:\\The\;midpoint\;of\;SQ:\;\\(\frac{-2+4}2;\frac{-2+4}2)\\T(1;1)\\\\The\;diagonals\;bisect\;one\;another\;{\vert\vert}^m\\\&\;perpendicularly\;so\\Therefore,\;PQRS\;is\;a\;rhombus\\\]
12.1\[m_{AE}=\frac{1-4}{2-0}\\=\frac{-3}2\\\&\\M_{EB}=\frac{3-1}{5-2}=\frac23\\\\m_{AE}\times m_{AB}=-1\\\\AE\perp EB\;\;"\widehat E=90^\circ"\]
12.2C(4; - 2) ... E midpoint AC & D(-l; -1) ... E midpoint BD
12.3
✓
✓
9. Determine the gradient of a straight line if it was
9.1 Parallel to the line given by 3x + 2y + 6 = 0, or
9.2 Perpendicular to that line.
10. The points A(1, 4), B(-2, -2), and C(4, 1) represent the vertices of triangle ABC on a Cartesian plane.
10.1 Calculate the coordinates of the midpoint D between points A and B. (2)
10.2 Derive the equation of the perpendicular bisector for the segment AB. (3)
10.3 Let E be the midpoint of AC; find the equation of the line segment BE. (2)
10.4 Prove that line segment DE is parallel to line segment BC. (3)
10.5 Compute the area of triangle ABC. (5)
10.6 Identify the coordinates of point M so that the sequence AMBC forms a parallelogram. (2)
Want To Master ####?
Sign up for free and complete the Mastery Quizzes with explained answers to deepen your understanding of this topic.
11. Triangle PRS has vertices at P(-1, 3), R(3, -1), and S(a, b), as illustrated in the provided diagram.
11.1 Demonstrate that the point T(1, 1) serves as the midpoint of the line segment PR. (1)
11.2 If the perpendicular bisector of PR intersects at point S, prove that a equals b. (4)
11.3 Given that , , and the area of the ∠PRS is 12 square units, determine the coordinates of point S. (8)
11.4 Since point Q(4, 4) is on the perpendicular bisector, discuss why the shape PQRS is classified as a rhombus. (4)
12. The vertises/points defining ∠ABE are A(0, 4), B(5, 3), and E(2, 1).
12.1 Show that angle Ê= 90°. (3)
12.2 Given that ABCD is a rhombus with diagonals AC and BD crossing at point E, find the coordinates of points C and D. (4)
12.3 Demonstrate that ABCD is a square, providing justifications. (4)
Need a Math tutor?
Start by joining our free sessions with professional math tutors, conducted entirely online for your convenience. Whether you’re at home or on the go, you won’t miss a thing our lessons are live and also recorded for easy access anytime. Plus, students can enquire with our tutors 24/7 for additional support.
13.
Determine:
13.1 the size of α. (2)
13.2 the size of β. (2)
13.3 the size of θ. (1)
Ask Plug Bot!
Try ask Plug Bot our AI that you can ask questions as you go through these notes, it is programmed with South African math curriculum content and it can explain concepts and answer your questions that are relevant to this topic.
MULTIPLICATION AND DIVISION OF FRACTIONS
Always remember that when you multiply fractions, you should multiply numerators with numerators and denominators with denominators.
\[\frac\alpha b\times\frac cd=\frac{\alpha\times c}{b\times d}\]You do not find a LCD when multiplying fractions.
You do not find the LCD (Lowest Common Denominator) when multiplying fractions.
Double Angles
In Grade 12, you are required to apply double-angle formulas to simplify trigonometric expressions and solve equations. Furthermore, you should also be able to derive and prove these double-angle formulas.
a. \[\cos2\mathrm A=\cos^2\mathrm A-\sin^2\mathrm A\\=2\cos^2\mathrm A-1\\=1-2\sin^2\mathrm A\]
b. \[2\sin2\mathrm A=2\mathrm{sinAcosA}\]
*For both a & b examples consider “A” as half the original angle of each
Proofs For Double Angle Formula
1. \[\mathrm{Show}\;\mathrm{that}\;\cos2\mathrm A=\cos^2\mathrm A\;-\;\sin^2\mathrm A\\\\\cos2\mathrm A=\cos(\mathrm A+\mathrm A)=\mathrm{cosAcosA}-\mathrm{sinAsinA}\\\cos^2\mathrm A-\sin^2\mathrm A\]
2. \[\mathrm{Derive}\;\mathrm{an}\;\mathrm{expression}\;\mathrm{for}\;\cos2\mathrm A\;\mathrm{using}\;\mathrm{only}\;\mathrm{cosA}\;\mathrm{and}\;\mathrm{sinA}\\\\\cos2\mathrm A=\cos^2\mathrm A-\sin^2\mathrm A\\=\cos^2\mathrm A-(1-\cos^2\mathrm A)\\=2\cos^2\mathrm A-1\]
Also get 100% on your exam essays!
Our essay cramming assistant is useful if you want to cram essays for subjects such as Business Studies, Economics, Geography, History, Home Languages, First Additional Languages and more…
